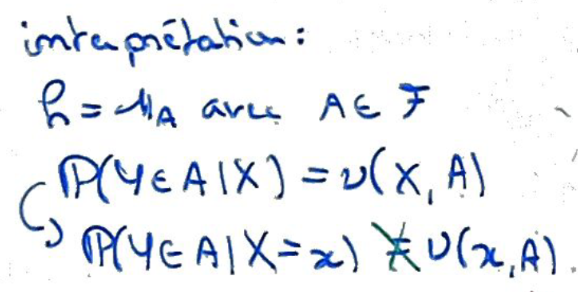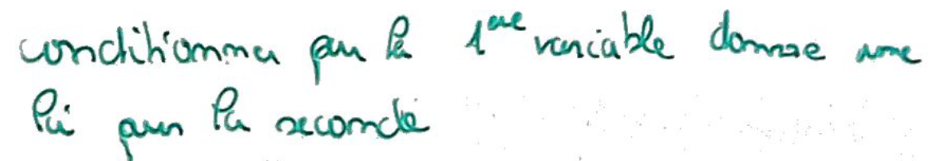Math'φsics

Menu
  • Acceuil
  • Maths
  • Physique
    • Maths
    • Physique
  • Loi conditionnelle

    Formulaire de report

    Loi conditionnelle \(\nu\) de \(Y\in(E,\mathcal E)\) sachant \(X\in(F,{\mathcal F})\)
    Probabilité de transition \(\nu(\cdot,\cdot)\) de \(E\) dans \(F\) qui a avec l'Espérance conditionnelle une formule similaire à celle du Théorème de transfert : $$\forall h:F\to{\Bbb R}_+\text{ mesurable}, {\Bbb E}[h(Y)|X]=\int\nu(X,dy)h(y)$$
    • formule pour le cas discret : $$\nu(x,A)=\begin{cases}{\Bbb P}(y\in A|X=x)=\cfrac{{\Bbb E}[\Bbb 1_{\{y\in A,X=x\} }]}{{\Bbb P}(X=x)}&\text{si}\quad{\Bbb P}(X=x)\gt 0\\ \delta_{y_0}(A)&\text{sinon.}&\end{cases}$$avec \(y_0\) un point fixé quelconque de \(F\)
    • formule pour le cas à densité : $$\nu(x,A)=\begin{cases}\displaystyle\frac1{q(x)}\int_Ap(x,y)\,dy&\text{si}\quad q(x)\gt 0\\ \delta_0(A)&\text{sinon.}&\end{cases}\quad\text{ avec }\quad q(x)=\int p(x,y)\,dy$$
    • formule dans le cas où \((X_1,\dots,X_n,Y)\) est un Vecteur gaussien : $$\nu((x_1,\dots,x_n),y)=q_\sigma\left( y-\sum^n_{j=1}\lambda_jx_j\right)\,dy$$


    Questions de cours

    START
    Ω Basique (+inversé optionnel)
    Recto: Donner une interprétation de la loi conditionnelle.
    Verso:

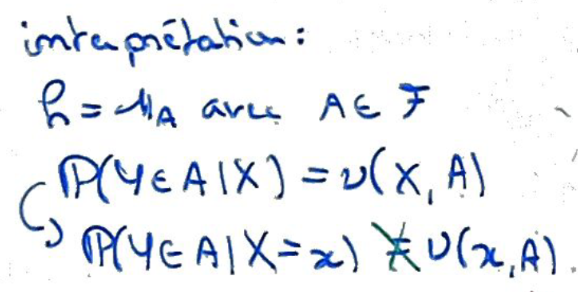
    Bonus:

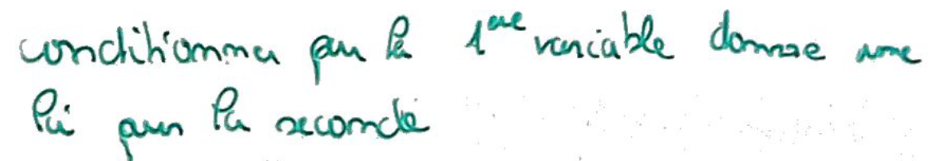
    Carte inversée ?:
    END

    Exercices


    On a la loi de \((X,Y)\).

    On a donc la loi de \(X\) en intégrant selon \(y\) (imagine qu'on connaissait l'aire).

    On reconnaît la loi.



    On sait que \(X\sim\mathcal Exp(a)\).

    On utilise la formule de la Probabilité conditionnelle pour exprimer la loi de \(Y|X\) en fonction de la loi de \(X\) et de la loi de \((X,Y)\).

    Exprimer la probabilité que \((X,Y)\in A\times B\) sous forme intégrale.

    Forcer l'apparition de la loi de \(X\) via un théorème belge.

    On reconnaît alors la densité de \(Y|X\).

    Et on reconnaît la loi.



    On a \(f_{Y|X}(x,y)=\frac{\Bbb 1_{0\lt y\lt e^{-ax} } }{e^{-ax} }\).

    On retrouve directement l'espérance conditionnelle en intégrant : $${\Bbb E}[Y|X]=\int yf_{Y|X}(X,y)\,dy$$



    On a \({\Bbb E}[Y|X]=\frac{e^{-aX} }2\) et \(X\sim\mathcal Exp(a)\).

    On a le résultat directement, en utilisant la formule : $${\Bbb E}[Y]={\Bbb E}[{\Bbb E}[Y|X]]$$



    On note que \(X_1+X_2\) suit la loi de Poisson de paramètre \(\lambda_1+\lambda_2\).

    Puisque la loi est discrète, on peut se contenter de calculer les probabilités de chaque événement individuellement.

    On reconnaît la loi.



    On modélise le problème par deux variables aléatoires.

    On a par hypothèse la loi de \(X|U\).

    Puisque \(X|U\) est discrète, le calcul est alors un calcul de probabilités conditionnelles discrètes.

    Pour tout intervalle, on peut obtenir \({\Bbb P}(U\in[a,b],X=0)\) via une formule de probabilité conditionnelle.

    On obtient le résultat voulu en prenant \(a=0\) et \(b=1\).


  • Rétroliens :
    • Espérance conditionnelle